Item Response Theory
Overview
The item response theory (IRT), also known as the latent response theory refers to a family of mathematical models that attempt to explain the relationship between latent traits (unobservable characteristic or attribute) and their manifestations (i.e. observed outcomes, responses or performance). They establish a link between the properties of items on an instrument, individuals responding to these items and the underlying trait being measured. IRT assumes that the latent construct (e.g. stress, knowledge, attitudes) and items of a measure are organized in an unobservable continuum. Therefore, its main purpose focuses on establishing the individual’s position on that continuum.
Description
Classical Test Theory
Classical Test Theory [Spearman, 1904, Novick, 1966]focuses on the same objective and before the conceptualization of IRT; it was (and still being) used to predict an individual’s latent trait based on an observed total score on an instrument. In CTT, the true score predicts the level of the latent variable and the observed score. The error is normally distributed with a mean of 0 and a SD of 1.
Item Response Theory vs. Classical Test Theory
IRT Assumptions
1) Monotonicity – The assumption indicates that as the trait level is increasing, the probability of a correct response also increases2) Unidimensionality – The model assumes that there is one dominant latent trait being measured and that this trait is the driving force for the responses observed for each item in the measure3) Local Independence – Responses given to the separate items in a test are mutually independent given a certain level of ability.4)Invariance – We are allowed to estimate the item parameters from any position on the item response curve. Accordingly, we can estimate the parameters of an item from any group of subjects who have answered the item.
If the assumptions hold, the differences in observing correct responses between respondents will be due to variation in their latent trait.
Item Response Function and Item Characteristic Curve (ICC)
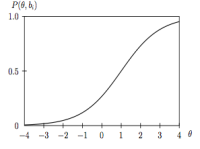
IRT models predict respondents’ answers to an instrument’s items based on their position on the latent trait continuum and the items’ characteristics, also known as parameters.Item response function characterizes this association.The underlying assumption is that every response to an item on an instrument provides some inclination about the individual’s level of the latent trait or ability. The ability of the person (θ) in simple terms is the probability of endorsing the correct answer for that item.As such, the higher the individual’s ability, the higher is the probability of a correct response. This relationship can be depicted graphically and it’s known as the Item Characteristic Curve. As is shown in the figure, the curve is S-shaped (Sigmoid/Ogive). Furthermore, the probability of endorsing a correct response monotonically increases as the ability of the respondent becomes higher. It is to be noted that theoretically, ability (θ) ranges from -∞ to +∞, however in applications, it usually ranges between -3 and + 3.
Item Parameters
As people’s abilities vary, their position on the latent construct’s continuum changes and is determined by the sample of respondents and item parameters. An item must be sensitive enough to rate the respondents within the suggested unobservable continuum.
Item Difficulty (bi) is the parameter that determines the manner of which the item behaves along the ability scale. It is determined at the point of median probability i.e. the ability at which 50% of respondents endorse the correct answer. On an item characteristic curve, items that are difficult to endorse are shifted to the right of the scale, indicating the higher ability of the respondents who endorse it correctly, while those, which are easier, are more shifted to the left of the ability scale.
Item Discrimination (ai) determines the rate at which the probability of endorsing a correct item changes given ability levels. This parameter is imperative in differentiating between individuals possessing similar levels of the latent construct of interest. The ultimate purpose, for designing a precise measure is to include, items with high discrimination, in order to be able to map individuals along the continuum of the latent trait. On the other hand, researchers should exercise caution if an item is observed to have a negative discrimination because the probability of endorsing the correct answer shouldn’t decrease as the respondent’s ability increases. Hence, revision of these items should be carried out. The scale for item discrimination, theoretically, ranges from -∞ to +∞ ; and usually doesn’t exceed 2; therefore realistically it ranges between (0,2)
Guessing (ci) Item guessing is the third parameter that accounts for guessing on an item. It restricts the probability of endorsing the correct response as the ability approaches -∞.
Population Invariance In simple terms, the item parameters behave similarly in different populations. This is not the case when following the CTT in measurement. As the unit of analysis is the item in IRT, the location of the item (difficulty) can be standardized (undergo linear transformation) across populations and thus items can be easily compared. An important note to add is that even after linear transformation, the parameter estimates derived from two samples will not be identical, the invariance as the name states refers to population invariance and so it applies to item population parameters only.
IRT Model Types
Unidimensional ModelsUnidimensional models predict the ability of items measuring one dominant latent trait.
Dichotomous IRT Models
The dichotomous IRT Models are used when the responses to the items in a measure are dichotomous (i.e. 0,1)
The 1- Parameter logistic model
The model is the simplest form of IRT models. It is comprised of one parameter that describes the latent trait (ability – θ) of the person responding to the items as well as another parameter for the item (difficulty). The following equation represents its mathematical form:
The model represents the item response function for the 1 – Parameter Logistic Model predicting the probability of a correct response given the respondent’s ability and difficulty of the item. In the 1-PL model, the discrimination parameter is fixed for all items, and accordingly all the Item Characteristic Curves corresponding to the different items in the measure are parallel along the ability scale. The figure shows 5 items, the one on the furthest right is the hardest and would be probably endorsed correctly by those with a higher ability.
Test Information Function
§ It is the sum of probabilities of endorsing the correct answer for all the items in the measure and therefore estimates the expected test score.
§ In this figure, it the red line depicts the joint probability of all 5 items (black)
The Item Information Function
Shows you the amount of information each item provides and it is calculated by multiplying the probability of endorsing a correct response multiplied by the probability of answering incorrectly.
It is to be noted that the amount of information at a given ability level is the inverse of its variance, hence, the larger the amount of information provided by the item, the greater the precision of the measurement. As item information is plotted against ability, a revealing graph depicts the amount of information provided by the item. Items measured with more precision, provide more information and are graphically depicted to be longer and narrower, compared to their counterparts that provide lesser information. The apex of the curve corresponds with the value of bi – the ability at the point of median probability. The maximum amount of information provided would be given when the probability of answering correctly or wrongly are equal, i.e. 50%. Items are most informative among respondents that represent the entire latent continuum and especially among those who have a 50% chance of answering either way.
Estimating Ability
The assumption of local independence, states that item responses should be independent and only associated via the ability. This allows us to estimate the individual response pattern’s likelihood function for the measure administered by multiplication of the item response probabilities. Next, through, an iterative process, the maximum likelihood estimate of ability is calculated. Simply, the maximum likelihood estimate provides us with the expected scores for each individual.
The Rasch Model vs. 1- Parameter Logistic Models
The models are mathematically equal, however, the Rasch Model constrains the Item Discrimination (ai) to 1, while the 1-Parameter logistic model strives to fit the data as much as possible and does not limit the discrimination factor to 1. In the Rasch Model, the model is superior, as it is more concerned with developing the variable that is being used to measure the dimension of interest. Therefore, when constructing an instrument fitting, the Rasch Model would be best, improving the precision of the items.
The 2- Parameter Logistic Model
The two parameter logistic model predicts the probability of a successful answer using two parameters (difficulty bi & discrimination ai).
The discrimination parameter is allowed to vary between items. Henceforth, the ICC of the different items can intersect and have different slopes. The steeper the slope, the higher the discrimination of the item, as it will be able to detect subtle differences in the ability of the respondents.
The Item Information Function
As is the case with the 1-PL Model, the information is calculated as the product between the probability of a correct and an incorrect response. However, the product is multiplied by the square of the discrimination parameter. The implication is that, the larger the discrimination parameter, the greater the information provided by the item. As the discriminating factor is allowed to vary between items, the item information function graphs can look different too.
Estimating Ability
With the 2-PL Model, the assumption of local independence still holds, and the maximum likelihood estimation of the ability, is used. Although, the probabilities for the response patterns are still summed, they are now weighted by the item discrimination factor for each response. Their likelihood functions, therefore, can differ from each other and peak at different levels of θ.
The 3 – Parameter logistic model
The Model predicts the probability of a correct response, in the same manner as the 1 – PL Model and the 2 PL – Model but it is constrained by a third parameter called the guessing parameter (also known as the pseudo chance parameter), which restricts the probability of endorsing a correct response when the ability of the respondent approaches -∞. As respondents reply to an item by guessing, the amount of information provided by that item decreases and the information item function peaks at a lower level compared to other functions. Additionally, difficulty is no longer demarcated at median probability. Items answered by guessing, indicate that the respondent’s ability is lesser than its difficulty.
Model Fit
One way to choose which model to fit, is to assess the model’s Relative fit through its Information criteria. AIC estimates are compared and the model with the lower AIC is chosen. Alternatively, we can utilize the Chi-squared (Deviance) and measure the change in 2*loglikelihood ratio. As it follows a chi-square distribution, we can estimate if the two models are statistically different from each other.
Other IRT Models
Include models that handle polytomous data, such as the graded response model, and the partial credit model. These models, predict the expected score for each response category. On the other hand, other IRT models like the nominal response models, predict the expected scores of individuals answering items with unordered response categories (e.g. Yes, No, Maybe). In this brief summary, we focused on unidimensional IRT models, concerned with the measurement of one latent trait, however these models wouldn’t be appropriate in the measurement of more than one latent construct or trait. In the latter case, use of multidimensional IRT models is advised. Please see the resource list below for more information about these models.
Applications
IRT models can be applied successfully in many settings that apply assessments (education, psychology, health outcome research, etc.). It can also be utilized to design and hone scales/measures by including items with high discrimination that add to the precision of the measurement tool and lessens the burden of answering long questionnaires. As IRT model’s unit of analysis is the item, they can be used to compare items from different measures provided that they are measuring the same latent construct. Furthermore, they can be used in differential item functioning, in order to assess why items that are calibrated and test, still behave differently among groups. This can lead research into identifying the causative agents behind differences in responses and link them to group characteristics. Finally, they can be used in Computerized Adaptive Testing.
Readings
Textbooks & Chapters
-
Hambleton, R. K., & Swaminathan, H. (1985). Item response theory principles and applications. Boston, MA: Kluwer-Nijhoff Publishing. Available here and here
-
Embretson, Susan E., and Steven P. Reise. Item response theory. Psychology Press, 2013. Available here
-
Van der Linden, W. J., & Hambleton, R. K. (Eds.). (1997). Handbook of modern item response theory. New York, NY: Springer. Available here
These three books (Item response theory principles and applications, Item response theory and Handbook of modern item response theory) provide the reader with the fundamental principals of IRT models. However, they don’t include recent updates and IRT software packages.
-
DeMars C. Item Response Theory. Cary, NC, USA: Oxford University Press, USA; 2010. Available here
In 138 pages, DeMars C. has succeeded in producing a succinct yet extremely informative resource that doesn’t fail to demystify the hardest of the IRT concepts. The book is an introductory book that addresses IRT assumptions, parameters and requirements and then proceeds to explain how results can be described in reports and how researchers should consider the context of test administration, respondent population and the effective use of scores.
-
Ayala RJd. The theory and practice of item response theory. (2009). Reference and Research Book News, 24(2). Available here
The theory and practice of item response theory is an applied book that is practitioner oriented. It provides a thorough explanation of both unideminsional and multidimensional IRT models, highlighting each model’s conceptual development, and assumptions. It then proceeds to demonstrate the underlying principles of the model through vivid examples.
-
Li Y, Baron J. Behavioral Research Data Analysis with R: Springer New York; 2012 (Chapter 8)
The book was developed with behavioral research practitioners in mind. It is provides help for them to navigate statistical methods using R. Chapter 8, focuses on Item Response Theory and offers a set of notes and a plethora of annotated examples.
-
A visual guide to item response theory by Ivailo Partchev, Friedrich-Schiller-Universität Jena (2004)
As the name suggests, the guide provides a visual representation of the basic concepts in IRT. Java applets permeate the text and make it easier to follow along while these basic concepts are explained. Excellent resource, and I would recommended reading it a couple of times and practicing on the applets!
-
Baker, Frank (2001). The Basics of Item Response Theory. ERIC Clearinghouse on Assessment and Evaluation, University of Maryland, College Park, MD
A one of a kind book, that focuses on offering the reader the joy of acquiring the basics of IRT theory without delving into mathematical complexities.
-
Thissen, D., & Wainer, H. (Eds.). (2001). Test Scoring. Mahwah, NJ: Lawrence Erlbaum.Available here and here
-
Lord, F.M. (1980). Applications of Item Response Theory to Practical Testing Problems. Hillsdale, NJ: Lawrence Erlbaum. Available here
-
Baker, F. B., & Kim, S. H. (2004). Item response theory: Parameter estimation techniques. New York, NY: Marcel Dekker. Available here and here
Methodological Articles
-
Lord, F. M. (1983). Unbiased estimators of ability parameters, of their variance, and of their parallel-forms reliability. Psychometrika, 48, 233-245
-
Lord, F. M. (1986). “Maximum Likelihood and Bayesian Parameter Estimation in Item Response Theory.” Journal of Educational Measurement 23(2): 157-162
-
Stone CA. Recovery of Marginal Maximum Likelihood Estimates in the Two-Parameter Logistic Response Model: An Evaluation of MULTILOG. Applied Psychological Measurement. 1992;16(1):1-16
-
Green, D. R., Yen, W. M., & Burket, G. R. (1989). Experiences in the application of item response theory in test construction. Applied Measurement in Education, 2(4), 297-312
Application Articles
-
Da Rocha NS, Chachamovich E Fau – de Almeida Fleck MP, de Almeida Fleck Mp Fau – Tennant A, Tennant A: An introduction to Rasch analysis for Psychiatric practice and research. (1879-1379)
The article’s main purpose is to describe Modern Test Theory (specifically Rasch analysis) in regards to designing instruments. The Beck Depression Inventory (BDI) is used as an example where depressive symptoms represent the latent variable being studied.
-
Cook KF, O’Malley KJ, Roddey TS. Dynamic assessment of health outcomes: time to let the CAT out of the bag? Health services research. 2005;40(5 Pt 2):1694-711
The article’s main objective is to introduce computer adaptive testing in the context of heath outcomes research. It also provides a simple, yet effective overview of the basics of IRT models.
-
Edwards MC. An Introduction to Item Response Theory Using the Need for Cognition Scale. Social and Personality Psychology Compass. 2009;3(4):507-29
The article’s main objective is to review the 2-PL Model and the Graded Response Model. The author illustrates the different features of both models via examples using the Need for Cognition Scale (NCS). Differential Item Functioning (DIF) and Computerized Adaptive Testing (CAT) are also briefly discussed.
-
Choi SW, Swartz RJ. Comparison of CAT Item Selection Criteria for Polytomous Items. 2009(0146-6216 (Print)).
The article’s main objective is to investigate item selection method properties, in the context of computer adaptive testing and polytomous items.
-
Rizopoulos, D. (2006). ltm: An R package for latent variable modeling and item response theory analyses. Journal of Statistical Software, 17 (5). 1-25
The article’s main objective is to present the “ltm” package in R which is instrumental in fitting IRT models. The ltm package focuses on both dichotomous and polytomous data. The paper provides illustrations using real data examples from the Law School Admission Test (LSAT) and from the Environment section of the 1990 British Social Attitudes Survey.
Software
For the complete list, please click on the following link:http://www.umass.edu/remp/software/CEA-652.ZH-IRTSoftware.pdf
Websites
Youtube tutorials (Extremely useful and informative)
-
A Conceptual Introduction to Item Response Theory: Part 1. The Logic of IRT Scoring
-
A Conceptual Introduction to Item Response Theory: Part 2. IRT Is a Probability Model
-
A Conceptual Introduction to Item Response Theory: Part 3. Plotting Along
-
A Conceptual Introduction to Item Response Theory: Part 4. Understanding Item Parameters
-
A Conceptual Introduction to Item Response Theory: Part 5. IRT Information
-
A Conceptual Introduction to Item Response Theory: Part 6. Applications of IRT
-
What is Item Response Theory? by Nick Shryane, ISC (The University of Manchester)
Courses
Courses offered at Mailman School of Public Health
-
P8417 – Selected Problems in Measurement
-
P8158 – Latent Variable and Structural Equation Modeling for Health Sciences